MCB128: AI in Molecular Biology (Spring 2026)

(Under construction)


block 1:

Feed Forward Networks / Protein 2D structure

In this block we introduce the Multilayer perceptron (MLP).

As a practical implementation of a MLP in molecular biology, we will study the work of Qian & Sejnowski (1988), “Predicting the secondary structure of globular proteins using neural network models” in which they use a MLP with one hidden layer to infer the secondary structure of globin proteins. This method is based on a previous work by the some of the same authors NetTALK applied to the problem of text-to-speech in which the inputs are strings of letters representing words and the outputs are sounds (phonemes). The MLP described by Qian & Sejnowski (1988) takes protein sequences as inputs, and reports as an output its secondary structure.

This is the code that implements the Qian-Sejnowski model.

Multilayer perceptron (MLP)

In the previous block 0, we discuss a one-neuron perceptron. We showed how perceptrons can work well as classifiers, when the inputs are linearly separable as in Figure9 of block 0. However, when the data is not linearly separable, it is provable that a simple perceptron cannot work. This result was introduced by Minsky & Papert in a book entitled “Perceptrons: An Introduction to Computational Geometry”, (1969).

Interestingly, that result halted research in neural networks for a while (the “ice age” of neural networks). The introduction of Multilayer perceptrons that can easily classify non-linearly separable, resolved the hiatus in the 1980s. I say interestingly, because Rosenblatt’s original perceptron paper from 1958 already includes “deep” neural networks with more than one layer of weights.

Generalization to many neurons, many layers and many outcomes

The single-neuron network can be easily generalized to be a fully connected neural network with many different outputs and going through many different layers from input to output.

The one-hot encoding of categorical variables

The states of our single-neuron network (active/inactive, apple/orange) can be easily rewritten using a one-hot representation.

\[\begin{aligned} \mbox{output/activity}\quad &\mbox{one-hot}\\ t = \{0,1\}\quad \quad &\bar t = [t_1, t_2]\\ t = 1\, \mbox{(Apple)} \quad &\bar t(A) = [1, 0]\\ t = 0\, \mbox{(Orange)}\quad &\bar t(O) = [0, 1]\\ \end{aligned}\]

This one-hot representation easily generalizes for a categorical variable with more than two outcomes \(\{t_1,\ldots t_O\}\) as,

\[\bar t_1 = [1,0,\ldots,0]\\ \bar t_2 = [0,1,\ldots,0]\\ \dot\quad \\ \dot\quad \\ \dot\quad \\ \bar t_O = [0,0,\ldots,1]\\\]

The output/activity: from a linear logistic function to softmax activation

The outcome of the single-neuron \(0\leq y\leq 1\)

\[y(\bar x,\bar W) = \frac{1}{1+ e^{-\sum_i x_i W_i}}\]

can be easily extended to

\[y_1(\bar x,\bar W^1) = \frac{1}{1+ e^{-\sum_i x_i W_i^1}}\\ y_2(\bar x,\bar W^2) = \frac{1}{1+ e^{-\sum_i x_i W_i^2}}\\\]

which can be easily converted to a \(2\)-dimensional probability outcome \(\bar p\),

\[\bar p = \{p_1,p_2\},\]

such that \(p_1 + p_2 = 1\), using the softmax function

\[p_1 = \frac{e^{y_1}}{e^{y_1} + e^{y_2}}\\ p_2 = \frac{e^{y_2}}{e^{y_1} + e^{y_2}}.\]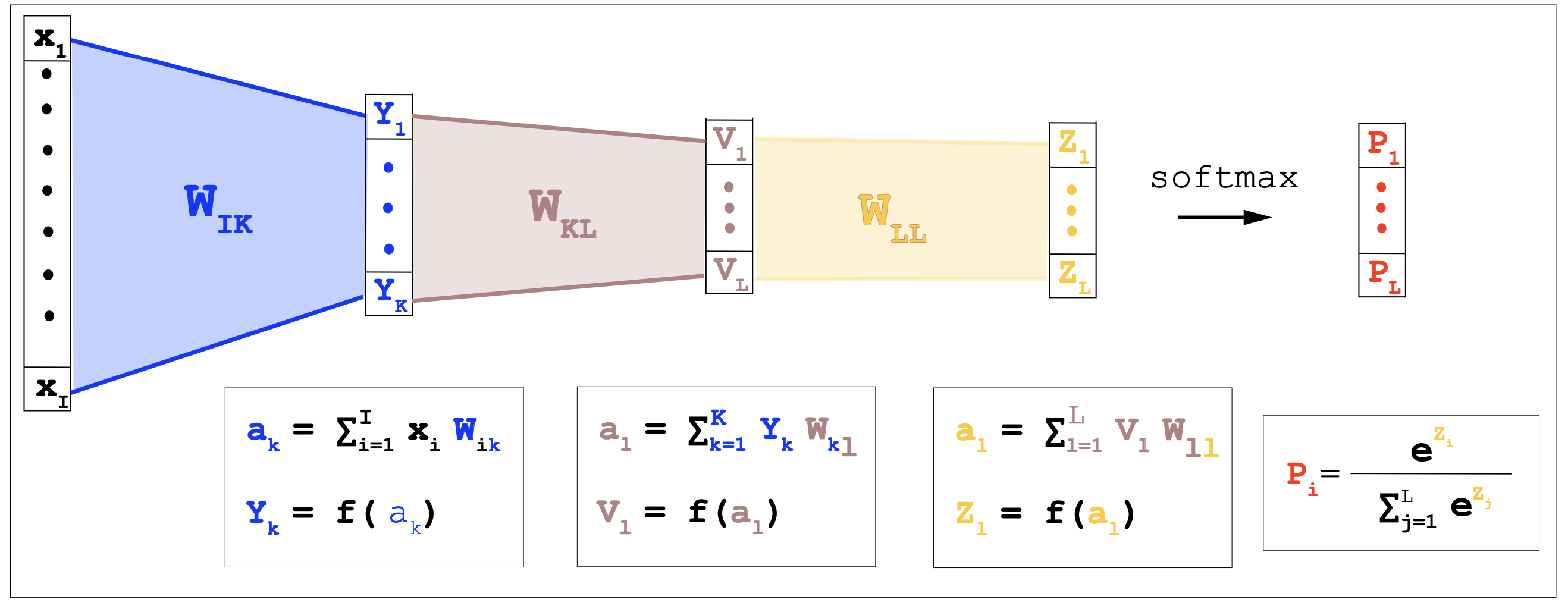

Figure 1. A fully connected neural network with two hidden layers.

Neural network with many outputs

The above result generalizes easily to a network with many possible outcomes.

A \(O\)-dimensional outcome \(\bar y\),

\[\bar y = \{y_1,\ldots, y_O\},\]

can be converted to a probability vector \(\bar p\) using the softmax function

\[\bar p = \{p_1,\ldots, p_O\},\]

such that

\[p_o = \frac{e^{y_o}}{e^{y_1} + \ldots + e^{y_O}}, \quad \mbox{and}\quad \sum_{o=1}^O p_o = 1.\]

And the loss function \(G\) easily generalizes to the cross entropy between the true outcomes \((t^{(n)}_1,\ldots, t^{(n)}_O)\) and the predicted outcomes \((p^{(n)}_1,\ldots, p^{(n)}_O)\) summed to all \(1\leq n\leq N\) cases in the training set.

\[G(w) = - \frac{1}{N}\sum_{n=1}^N \sum_{o=1}^O t^{(n)}_o \log p^{(n)}_o(w).\]

A fully connected (FC) layer

A fully connected (FC) layer connects every input in the previous layer to every output in the next layer.


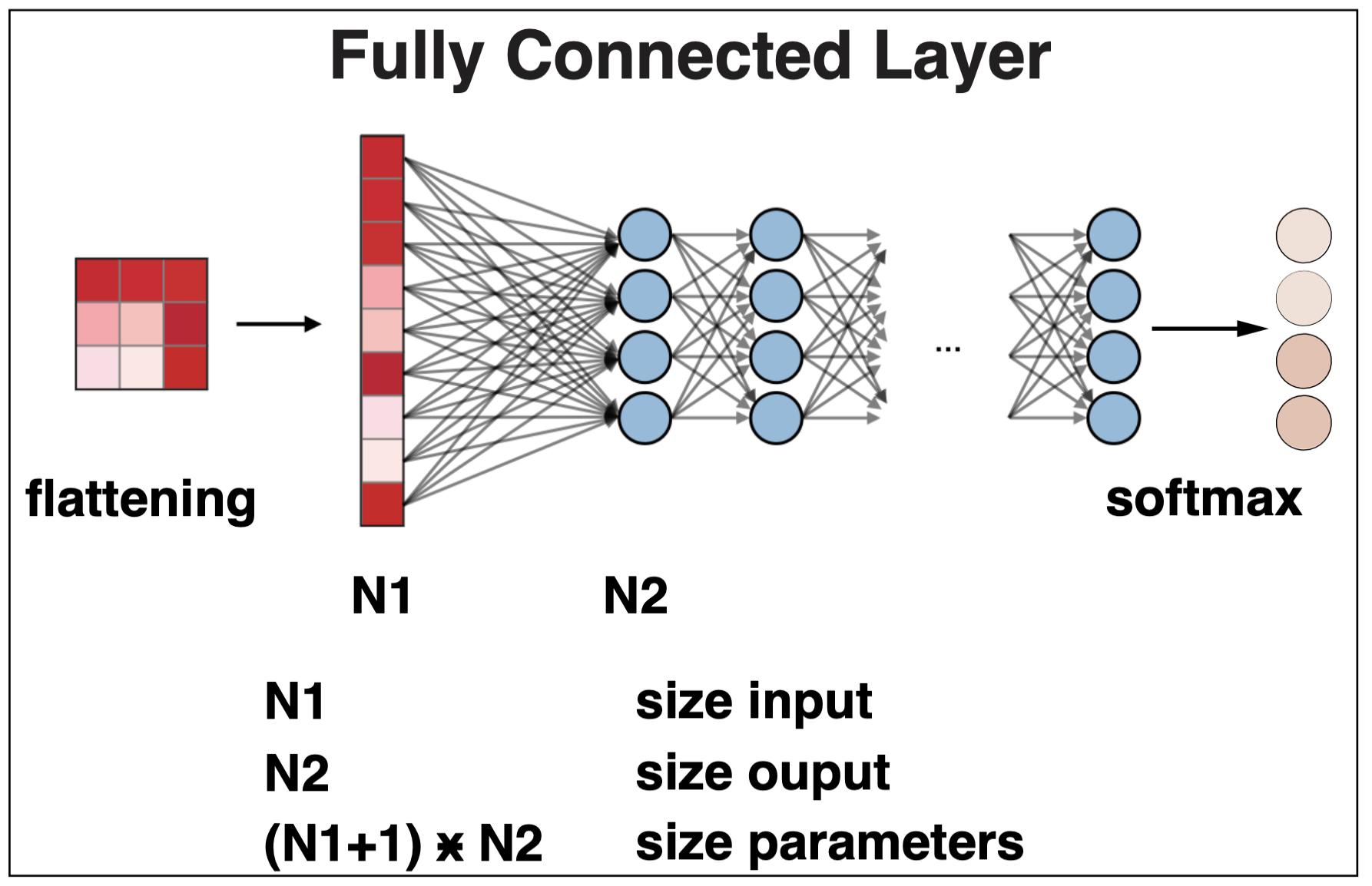
Figure 1. A fully connected layer. For an input layer of dimension N1, and an output layer of dimension N2, the weights of a FC layer have dimension N1*N2, plus a bias of dimension N2.

FC layers are typically used at the end of o a neural network to perform the final classification.

Protein 2D structure

In this section, we describe in detail the MLP with one hidden layer “Predicting the secondary structure of globular proteins using neural network models”, introduced by Qian & Sejnowski in 1988.

Protein secondary structure can be calculated based on its atoms’ 3D coordinates once the protein’s 3D structure is solved using X-ray crystallography or NMR. However, X-ray or NMR is expensive. Ideally, we would like to predict the secondary structure of a protein based on its primary sequence directly, which has had a long history.

The secondary structure of a given protein is described in Figure 2. It consists of mainly three possible local configurations that repeat over and over again: the alpha-helix, the beta-sheets and finally the random coil. The protein 2D structure is an intermediate between the protein sequence and the actual 3D structure.


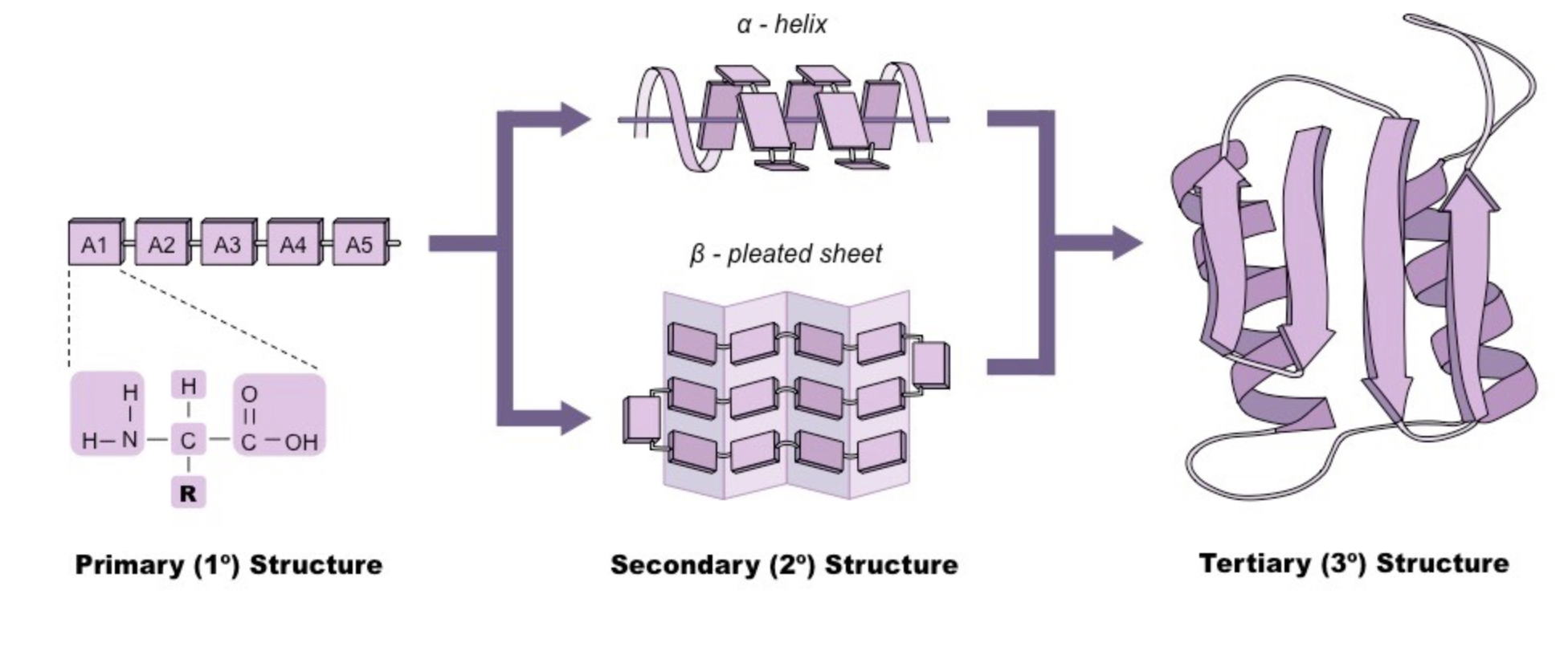
Figure 2. Protein structure: from amino acid sequences (1D) to alpha-helix, beta-sheet and random coil (2D) to all atom's representation (3D).

The Qian-Sejnowski Model

The Qian-Sejnowski protein 2D structure model is an example of a MLP with one hidden layer described in Figure 3.

Here is the code that implements the Qian-Sejnowski model.

Input layer

The inputs are sliding windows of 13 contiguous amino acids in the protein sequence. Each amino acid is described by a 21 one-hot encoding, for 20 amino acids and one more for a spacer. The spacer is used in training, where all training protein sequences are joined together connected by spacers.

We represent the input layer with \(x\) with dimensions \([N,I]\), where \(N\) is the number of total windows used in training, and \(I=13\) in this example.

Output Layer

For each input, the output is a 3-class softmax prediction for alpha helix (H) , beta sheet (B) or random coil (C).

\[H = [1,0,0]\\ B = [0,1,0]\\ C = [0,0,1]\]

We represent the outputs with \(y\) with dimensions \([N,O]\), where \(N\) is the number of total windows used in training, and output dimension \(O=3\) is the three classifications of protein 2D structure.

Hidden layer

The hidden layer connects the input with the output layer. The variables of the hidden layer \(h\) have dimension \([N,H]\). The variables of the hidden layer are the outputs of the previous layer (the Input layer here), and the inputs of the next layer (the Output layer in this case).

The weights

The parameters of the models are two sets of weights and biases:

Network

The network is a MLP with one hidden layer, as the one described in Figure 3. In the Qian-Sejnowski model, the input dimension is 13, the hidden dimension is 40, and the output dimension is 3.

Instead of a RELU function (as in Figure 3), the Qian-Sejnowski model uses as activation function the linear logistic function


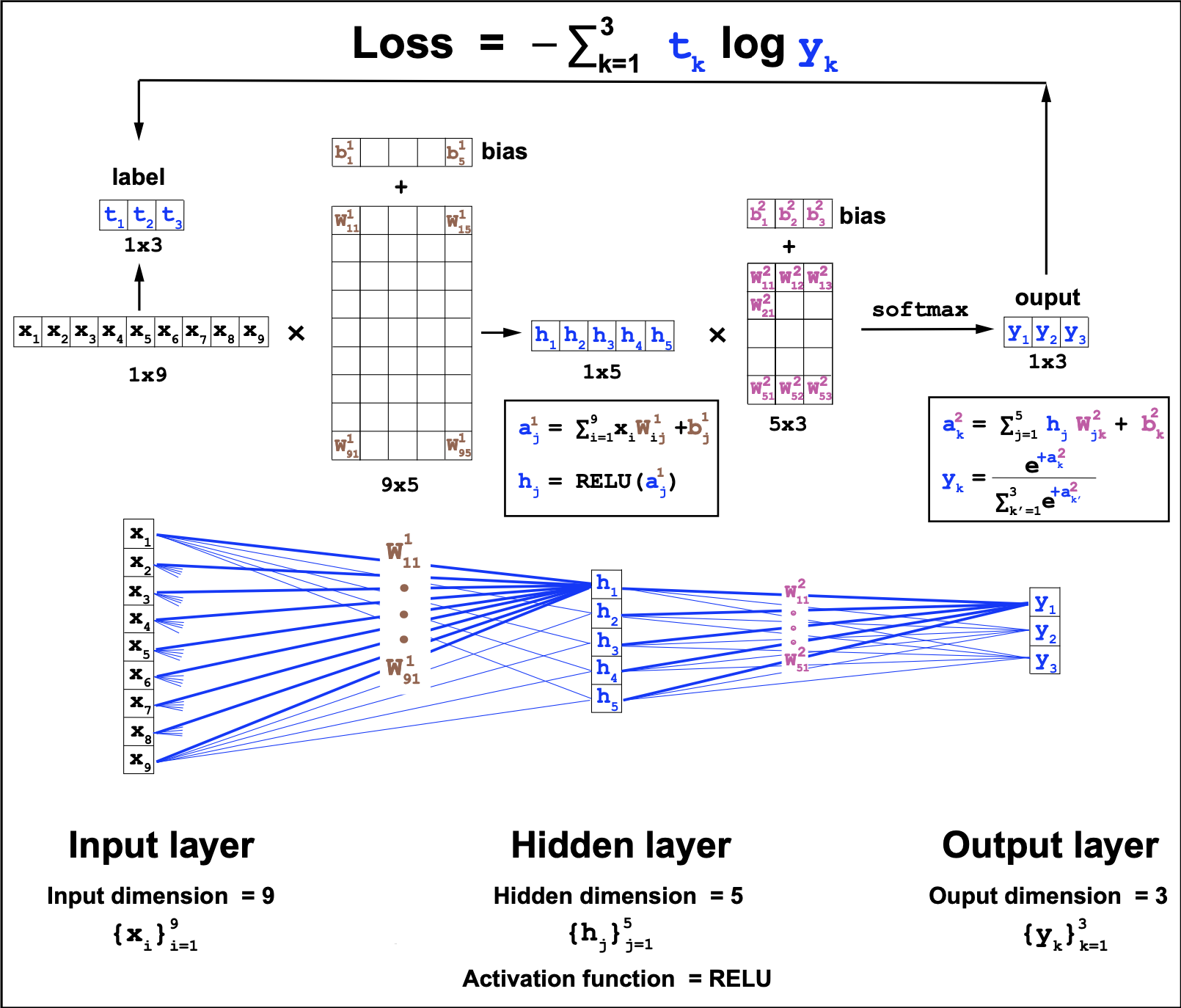
Figure 3. Multilayer perceptron with one hidden layer. This is a fully connected feed forward network. This particular MLP uses the RELU] logistic function. The input dimension of 9, the hidden layer dimension is 5, and the output dimension is a 3-class softmax.

The data

The data is a collection of protein sequences annotated with their secondary structure in the form of three states: alpha helix (H), beta strand (or sheet) (E) or random coil (C). Qian and Sejnowski used globin proteins. Here we are using the casp13, cb513 and ts115 datasets.

sliding one-hot windows

Each protein is split into 13 amino acid windows, moving one amino acid at the time. The inputs are all the 13 amino acid windows, and the output is a 3-class probability vectors describing the secondary structure (H, E or C) of the amino acid in the middle of the window.

The loss function

The loss function is the cross entropy between the true outcomes \((t^{(n)}_1,\ldots, t^{(n)}_O)\) and the predicted outcomes \((y^{(n)}_1,\ldots, y^{(n)}_O)\) summed to all \(1\leq n\leq N\) cases in the training set.

\[L(W^1, b^1, W^2, b^2) = - \frac{1}{N}\sum_{n=1}^N \sum_{o=1}^O t^{(n)}_o \log y^{(n)}_o.\]

The predicted outcomes \(y^{(n)}_o\) depend on all the weight parameters \(W^1, b^1, W^2, b^2\) as described in Figure 3.

Training. Update of the parameters by stochastic gradient descent (SGD)

The parameters of the model are updated using stochastic gradient descent, that is the weights are updated iteratively (each iteration is called a epoch), and at each epoch, all the weights are modified by a quantity proportional to the negative loss change as a function of the parameters, that is, against the gradient or gradient descent

\[\begin{aligned} W^1_{ij} &\longleftarrow W^1_{ij} - \alpha \frac{\partial L}{\partial W^1_{ij}}\quad 1\leq i \leq I\\ b^1_{j} &\longleftarrow b^1_{j} - \alpha \frac{\partial L}{\partial b^1_{j}} \quad 1\leq j \leq H\\ W^2_{jk} &\longleftarrow W^2_{jk} - \alpha \frac{\partial L}{\partial W^2_{jk}}\quad 1\leq k \leq O\\ b^2_{k} &\longleftarrow b^2_{k} - \alpha \frac{\partial L}{\partial b^2_{k}}. \end{aligned}\]

The meta-parameter \(\alpha>0\) is called the learning rate, and it is usually set to some small value such as \(0.1\).

The gradient descent process is not necessarily guarantee to converge to a minimum, but it often does. Results depend on many factor such as the learning rate, the database and the loss used. When you train a model, you watch the loss and how it decrease, and based on that, make a decision on when to stop the training and set on a value of the weight parameters.

Calculating the derivatives of the loss with respect to the different parameters is usually done by a method called backpropagation that we move to describe next in detail of our MLP with one fully connected hidden layer.

Backpropagation with one hidden layer

Because the Loss depends on all the parameters indirectly, calculating the derivatives of the Loss with respect to the parameters requires using the chain rule several times. That process is that in the field is referred to as backpropagation.

For this simple case of only one hidden layer, we are going to do the backpropagation explicit in the next section. Lucky for us PyToch does the backpropagation for us. This is the code that implements the Qian-Sejnowski model both in python using explicit calculations of the gradients, and in PyTorch.

Using explicit calculations of the gradients

Using the notation introduced in Figure 3 for the 1 hidden layer MLP, we need to go backwards starting from the \(W^2\) and \(b^2\) weights. The Loss depends on those as

\[L \rightarrow y \rightarrow a^2 \rightarrow W^2, b^2\]

we can write,

\[\begin{align} d W^2 := \frac{\partial L}{\partial W^2} &= \frac{\partial L}{\partial a^2} \frac{\partial a^2}{\partial W^2} = d a^2 \frac{\partial a^2}{\partial W^2}\\ d b^2 := \frac{\partial L}{\partial b^2} &= \frac{\partial L}{\partial a^2} \frac{\partial a^2}{\partial b^2} = d a^2 \frac{\partial a^2}{\partial b^2} \end{align}\]

We leave for the appendix to show that for a the cross-entropy loss and \(y=\mbox{softmax}(a^2)\), then

\[da^2 := \frac{\partial L}{\partial a^2} = y - t.\]

Figure 4. Backpropagation for weights W2

Then

\[\begin{align} d W^2_{jk} &= \sum_{k^\prime} d a^2_{k^\prime} \frac{\partial a^2_{k^\prime}}{\partial W^2_{jk}} = d a^2_{k}\, h^1_j \\ d b^2_{k} &= \sum_{k^\prime} d a^2_{k^\prime} \frac{\partial a^2_{k^\prime}}{\partial b^2_{k}} = d a^2_{k} \end{align}\]

In matrix notation:

\[\begin{align} d W^2[H,O] &= (h^1)^T[H,N] \cdot (y-t)[N,O]\\ d b^2[O] &= sum (y-t)[N,O] \end{align}\]

For \(W^1\) and \(b^1\), the dependencies are

\[L \rightarrow y \rightarrow a^2 \rightarrow h \rightarrow a^1 \rightarrow W^1, b^1\]

then,

\[\begin{align} d W^1 := \frac{\partial L}{\partial W^1} = & \frac{\partial L}{\partial a^1} \frac{\partial a^1}{\partial W^1} = da^1 \frac{\partial a^1}{\partial W^1} = da^1 \cdot X\\ d b^1 := \frac{\partial L}{\partial W^1} = & \frac{\partial L}{\partial a^1} \frac{\partial a^1}{\partial b^1} = da^1 \frac{\partial a^1}{\partial b^1} = da^1\\ \end{align}\]

Figure 5. Backpropagation for weights W1

We use again the chain rule to calculate \(da^1\) as

\[da^1 := \frac{\partial L}{\partial a^1} = \frac{\partial L}{\partial h^1} \frac{\partial h^1}{\partial a^1} = d h^1 \cdot \frac{d\mbox{RELU}(a^1)}{d a^1}\]

and \(dh^1\) can be calculated as a function of \(da^2\) as

\[dh^1 [N,H] := \frac{\partial L}{\partial h^1} = \frac{dL }{\partial a^2} \frac{\partial a^2}{ \partial h^1} = da^2[N,O] (W^2)^T[O,H]\]

Finally,

\[dW^1 [I,H] = (X)^T[I,N] \cdot da^1 [N,H]\]

Automatic backpropagation using PyTorch

The backpropagation calculation that we did for a MLP with one layer can be extended to more layer, but become very inefficient very quickly, specially considering that most models include large numbers of layers. PyTorch and other machine learning libraries become very practical as they are able to perform the backpropagation step to calculate all the parameters gradients automatically.


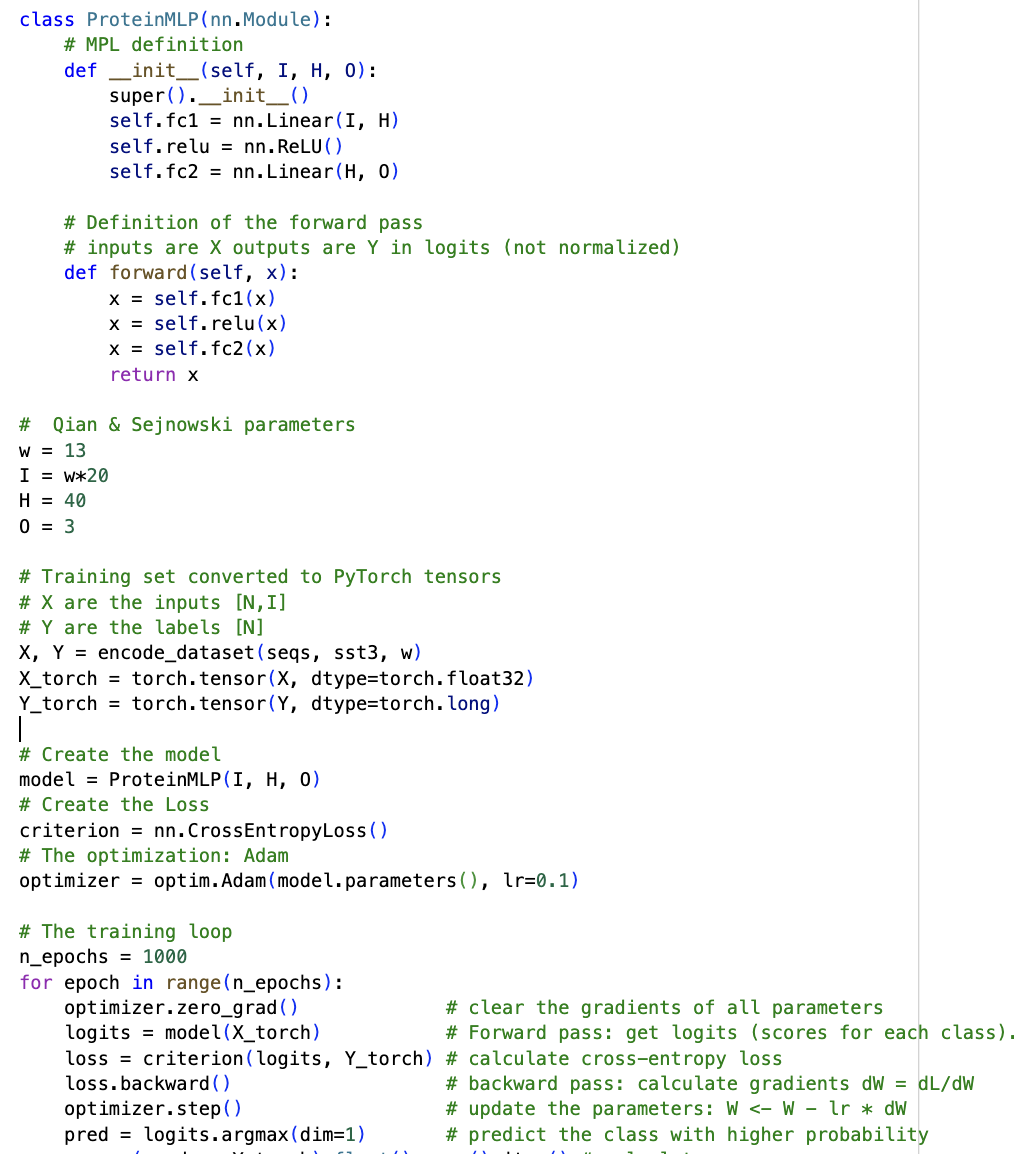
Figure 6. MLP with one hidden layer in PyTorch.

In PyTorch, one just needs to specify the Loss as a function of the weights and inputs, and it does the calculation of the gradients (vector of derivatives) automatically. As described in Figure 6, the steps are

For 1000 epochs:

Here is the code that implements the Qian-Sejnowski model both in python using explicit calculations of the gradients, and in PyTorch.


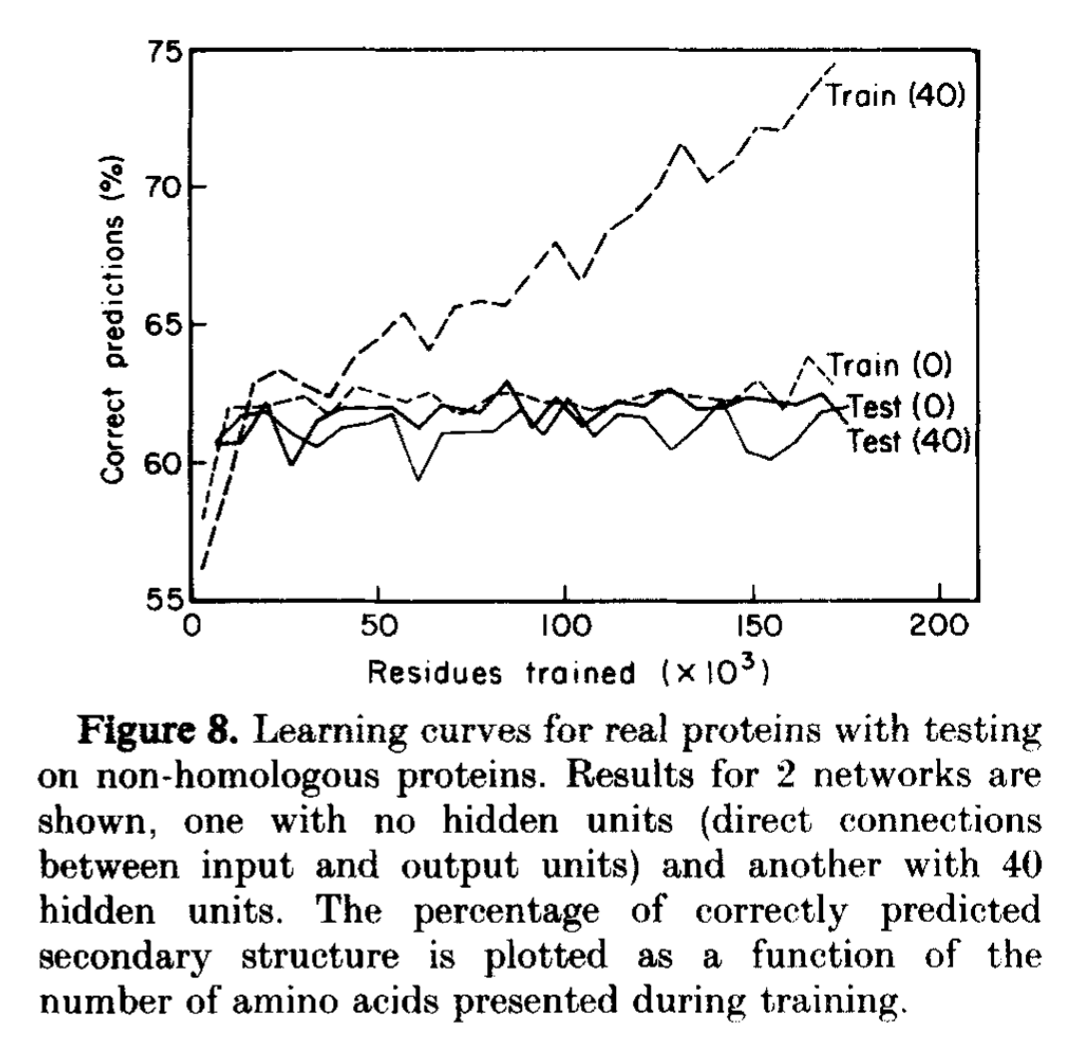
Figure 8 from Qian \& Sejnowski, 1988. Train(40) and test (40) results correspond to their 1 layer MLP with dimension 40 for the hidden layer. Train(0)/Test(0) are results using a perceptron with no hidden layers.

Overfitting

This paper already introduces the concept of overfitting. Overfitting refers to the fact that as models have more and more parameters, they become better and better to fit the parameters to the training date, to the point that those parameters do not perform well on a new example input that has not been seen in the training set before.

In the Qian-Sejnowski, they are careful train their model on one set of globing sequence, and they test on a different set of globins that has no sequence similarity (homologs) to the training set. See Figure 8 of paper reproduced here. Notice how the performance of test(40) is much lower than that of the training set train(40).

Fundamentals of neural networks

Figure 7 describe some of the basic elements of most deep learning methods.


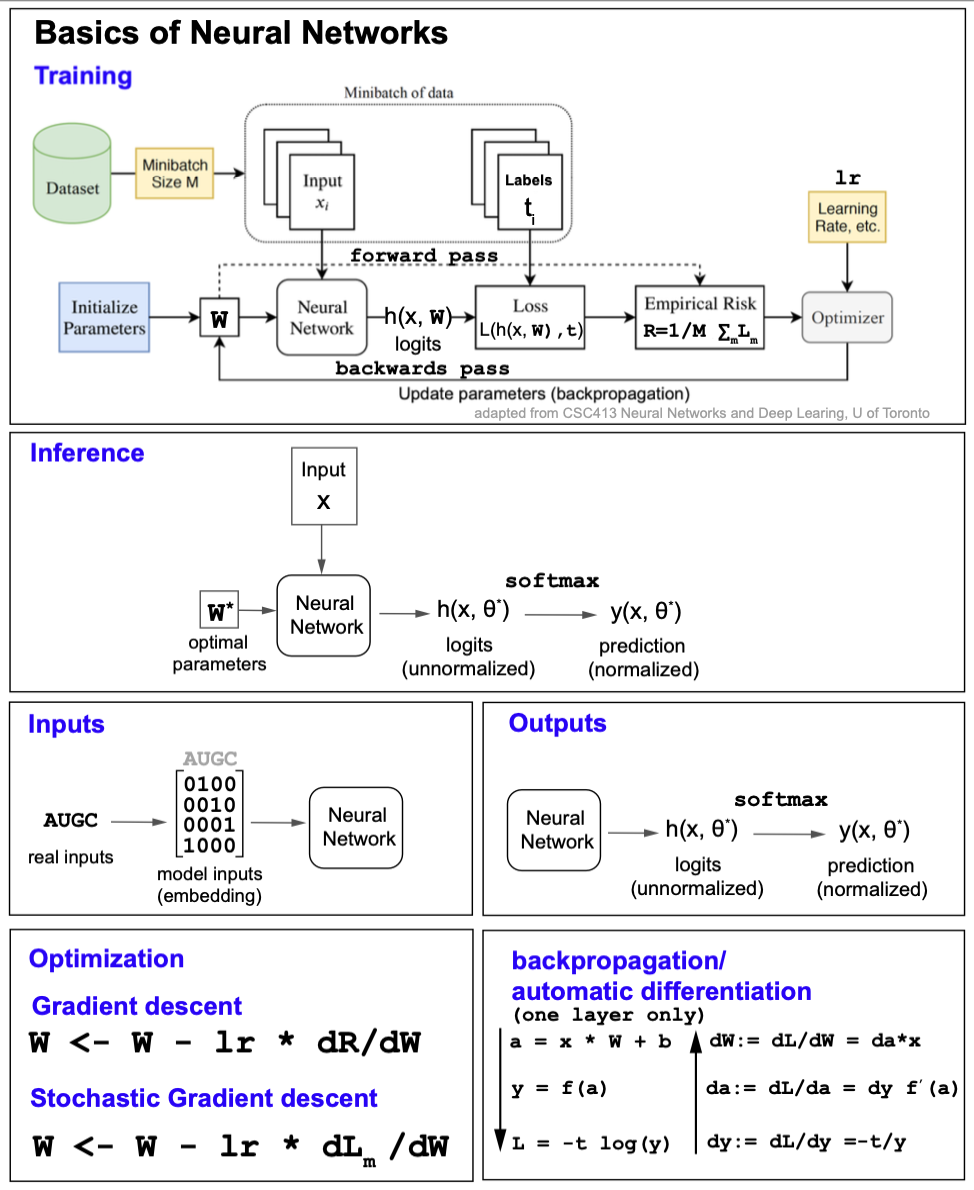
Figure 7. Fundamentals of neural networks.

Training

The basic elements of training are

The training set

The dataset used for training the parameters which includes the inputs (\(x\)) and labels (\(t\)) used for supervised learning.

Minibatch

To include randomness in the process, not all the training examples are used at once, at each training iteration (epoch), a different subset of training examples is used (a minibatch). There is usually a trade-off between the size of the minibatch,, the accuracy of the optimization and generalization. As the minibatch size increases, the accuracy of the gradients also increases, but the accuracy of the model predicting previously unseen cases (generalization) may decrease.

Weights’ initialization

The weights of the model are usually initialized to random numbers at the start of the training process. It is important to be aware that different initializations may affect the gradients and the optimization process. Also, weights should not be initialized to very large of very small values, as that may result in exploding gradients or vanishing gradients respectively.

Optimization

The optimization of the parameters \(W\) is performed by minimizing a loss function which measures how the outputs of the network for the training set \(y_m\) are different from the labels \(t_m\).

\[W^\star =\mbox{argmin}_{W} L\left(y(x,W), t\right)\]

It is standard to perform the parameter’s update towards a minimum by gradient descent, where the parameters are modified by a quantity proportional to the gradient of the loss.

The parameters at the next iteration \(k+1\) are given as a function of the parameters at the current \(k\) iteration as

\[W^{k+1} \leftarrow W^k - \alpha \frac{\partial L \left(y(W^{k})\right) }{\partial W}.\]

The learning rate

The learning rate is the positive proportionality constant \(\alpha > 0\) between the change of the parameters and the loss gradient. The learning rate should not be to large (the gradients will blow up) or too small (changes are too small and it takes for ever to converge).

It is quite frequent and standard to use for automatic optimization a method called Adam, which is a refinement of the expression above. In Adam optimization, instead of a fixed learning rate \(\alpha\), there is a learning rate scheduler, such that the actual learning rate also changes at each epoch.

Backpropagation

Backpropagation is the name given to calculate the loss gradients respect to the parameters.

The loss does not depend explicitly from the weights, thus we need to apply the chain rule to backprogate the errors. This is also referred to as the backward pass.

As an example, for the case of a of a MLP with one hidden layer, backpropagation works as follows,

In the forward pass (left) given the inputs and weights, the outputs \(y\) and all intermediate values are calculated. Then, introducing the notation \(d v := \frac{\partial L}{\partial v}\), we can compute the gradients of loss wrt the weights by using those values in the backward pass (right).


Figure 8. Calculation of the derivatives computed directly from the values obtained by the forward pass (rather than as a mathematical operation). Notation: dv := dL/dv.

Using PyTorch once the model has been define and the loss has been calculated, the backpropagation step is done automatically simply declaring “loss.backward()”.

Inference

At inference, there are only inputs, but not labels. We use the best set of parameters previously trained by the model, and we use a forward pass to calculate the output of the model, which are the predictions.

Inputs

The inputs need to be converted into a numerical representation, or embedding. A typical embedding is a onehot. Other more complicated embedding could be the output of a language model.

Outputs

The outputs as they come out of the last layer of the model are usually unnormalized. In general, there is one final softmax conversion to convert them into a probability distribution amongst all possible outcomes.

Appendix

Here we show that for the cross-entropy loss

\[L = - \sum_k t^k \log y^K\]

such that the predictions \(y\) are a softmax,

\[y = \frac{\exp{a^k}}{\sum_{k^\prime} \exp{a^{k^\prime}}},\]

and the labels \(t\) are one-hot encoded

\[\sum_k t_k = 1\]

then

\[d a_k := \frac{\partial L}{\partial a^k} = y^k - t^k.\]

Using the chain rule

\[d a^k := \frac{\partial L}{\partial a_k} = \sum_{k^\prime} \frac{\partial L}{\partial y_{k^\prime}} \frac{\partial y_{k^\prime}}{da_k}.\]

We can see that

\[d y_{k^\prime} := \frac{\partial L}{\partial y_{k^\prime}} = - \frac{t_{k^\prime}}{y_{k^\prime}}\]

Also

\[\frac{\partial y_{k^\prime}} {a_k} = \delta_{k {k^\prime}} y_{k^\prime} - y_k y_{k^\prime} = y_{k^\prime} \left(\delta_{k {k^\prime}} - y_k\right)\]

thus,

\[\begin{align} \partial a^k &= \sum_{k^\prime} - \frac{t_{k^\prime}}{y_{k^\prime}} y_{k^\prime} \left(\delta_{k {k^\prime}} - y_k\right)\\ &= -\sum_{k^\prime} t_{k^\prime} \,\left(\delta_{k {k^\prime}} - y_k\right) = -t_k + y_k\,\sum_{k^\prime} t_{k^\prime} \\ &= y_k - t_k. \end{align}\]

as the labels \(t[1,O]\) are one-hot encoded.